Comprei um HD de 500GB. Afinal, o que isso significa exatamente?
3 maio 2023Voltemos no tempo um 50 mil anos, quando o ser humano começou a contar. Vamos imaginar um homem primitivo querendo registrar quantos carneiros havia no rebanho, para conferir no dia seguinte se faltava algum. Para isso, precisava de objetos que representassem os carneiros. Para cada carneiro, ele separaria um objeto, e o conjunto de objetos ficaria representando o conjunto de carneiros.
Ele poderia usar pedrinhas para isso.

No entanto, em vez de pedras, nosso pastor tinha outros objetos mais facilmente disponíveis: os dedos de sua mão. Assim, para cada carneiro, ele dobrava um dedo da mão.

E se acabassem os dedos depois de usar as duas mãos? Ele poderia iniciar a contagem novamente sucessivas vezes com os dedos, sempre lembrando quantas vezes tinha reiniciado, novamente associando cada reinício com um dedo. Dessa forma, a contagem progride em rodadas de 10, que são reunidas em grupos de 10 contagens, e assim por diante.
Bem, depois de contar os carneiros, nosso matemático antigo não iria querer manter os dedos na mesma posição até a manhã seguinte para checar novamente os carneiros. Em vez disso, ele iria desenhar uma figura representando os dedos. Essas figuras acabaram evoluindo para se tornarem os numerais arábicos que viemos a usar depois.
Neste artigo, vou pular a longa e fascinante história do zero, uma das mais importantes abstrações concebidas pelos seres humanos. Em vez disso, darei um enorme salto lá do pastor antigo para o sistema numérico que usamos hoje, chamdo “sistema decimal”, que utiliza dez símbolos, incluindo o zero, para representar dez diferentes quantidades básicas: 0,1,2,3,4,5,6,7,8,9.
Usando numerais em vez de dedos da mão, fica fácil registrar o número de vezes que reiniciamos a contagem de dez. Basta adicionar um numeral na frente da contagem atual, representando quantos grupos de dez já estão acumulados.
1 grupo de dez já contado: 10, 11, 12, 13, 14…
2 grupos de dez já contados: 20, 21, 22, 23, 24…
Alguém no mundo antigo associou aos elementos dessa contagem a palavra “digitus” (dedo, em latim). Assim, hoje chamamos os numerais decimais de “dígitos”.
Mas, por volta de 1940, como parte do esforço de guerra, cientistas da Alemanha, dos Estados Unidos e da Inglaterra concentraram-se em projetos de máquinas poderosas para fazer cálculos (que os norte-americanos denominaram “computers”). Veja nosso artigo sobre os primeiros computadores.
Inicialmente, tentaram-se criar máquinas que operassem no sistema decimal, mas logo perceberam que ele é terrivelmente complicado para ser usado em uma máquina, já que máquinas não têm algo similar a mãos com 10 dedos. Para representar numerais decimais em uma máquina eletrônica seria preciso usar, por exemplo, 10 diferentes níveis de voltagem em um circuito. Operar com esse tipo de dados seria um pesadelo de engenharia.
No universo das máquinas eletrônicas, a forma mais natural de contar objetos é algo como uma lâmpada: para registrar um carneiro, acende-se uma lâmpada. O segundo nível de contagem pode ser uma segunda lâmpada, e assim por diante. Evidentemente, é preciso muitas lâmpadas para isso, mas isso não torna o sistema complexo. Independentemente do número de lâmpadas, o sistema é essencialmente simples. E muitíssimo mais simples de implementar que o sistema decimal.
A figura seguinte mostra como se podem contar carneiros usando uma fileira de lâmpadas. Você pode supor que há quantas lâmpadas forem necessárias.

Não vou tentar explicar a lógica dessa contagem aqui, pois a explicação seria mais complicada que a própria lógica. Sugiro que você gaste um tempo observando a figura anterior. Certamente, você entenderá a regra.
Assim, desenvolveu-se um sistema de contagem no qual o elemento contador básico (lâmpada, no nosso exemplo) tem apenas dois estados, em vez de dez (nossas mãos). Para diferenciar esse sistema do sistema decimal, ele foi chamado “sistema binário”. O conjunto de numerais necessários para esse sistema contem apenas dois elementos. Tomaram-se emprestados os primeiros numerais do sistema decimal, adotando-se para o sistema binário os numerais “0” e “1”. Observando a figura anterior, podemos criar uma tabela relacionando os primeiros números nos sistemas decimal e binário:
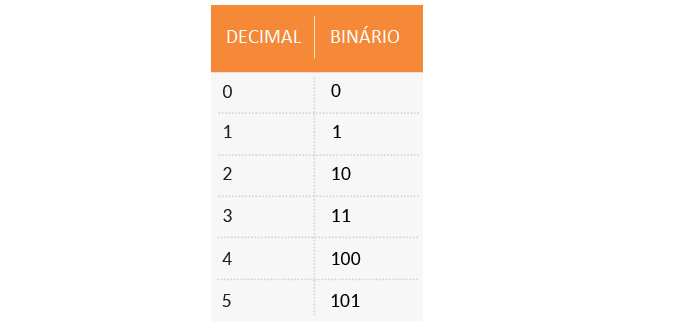
Embora esse sistema numérico possa parecer complicado para nós pois estamos acostumados com os números decimais, ele é, na verdade, muito mais simples. Foi essa invenção o que abriu caminho para o desenvolvimento dos computadores.
Mesmo não sendo derivado do uso de dedos, o sistema binário manteve a palavra “digito” para seus numerais, que são então chamados “digitos binários”. Como consequência, os equipamentos que usam esse sistema são ditos “digitais”. Ou seja, um equipamento digital é qualquer dispositivo eletrônico que representa internamente os números no sistema binário. Os computadores foram os primeiros equipamentos digitais.
Cada dígito binário é chamado de “bit” (abreviação de “binary digit”).
E quais dispositivos físicos são usados para identificar esses dois estados em um computador? Um computador não usaria lâmpadas para isso, já que ele não opera a partir de informações visuais. Os primeiros computadores utilizaram dispositivos chamados “válvulas eletrônicas”, que controlam correntes elétricas como se fossem torneiras que abrem e fecham. Por exemplo, a ausência de corrente elétrica representa “0” e a presença da corrente representa “1”.

Hoje, os bits são empacotados em dispositivos microscópicos, construídos em pastilhas de silício por meio de reações químicas, e que formam os chips. Um chip com alguns milímetros quadrados pode armazenar bilhões de dígitos binários.

No entanto, além de números, computadores operam também com letras e sinais gráficos. Como representar tantos elementos com apenas dois símbolos?
A solução foi usar os símbolos em grupos.
Logo no início do desenvolvimento dos computadores, os cientistas concluiram que grupos de 8 dígitos binários geravam um número de combinações suficientes para representar todos os algarismos decimais, letras e sinais gráficos. Assim, adotou-se o grupo de 8 dígitos como o elemento básico de informação nos computadores.
Um grupo de 8 bits foi chamado de “byte”. Abaixo vemos alguns exemplos de bytes:
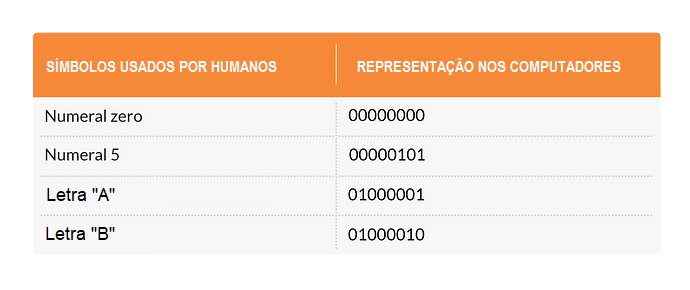
Comparando essa tabela com a tabela anterior, você vê que os numerais decimais são os números binários correspondentes, com uma série de dígitos “0” acrescentados à esquerda para completar os 8 bits. As outras combinações são usadas para letras, símbolos gráficos etc.
Além de letras e números, os pixels da tela e as instruções de programação em linguagem de máquina também são representados em bytes. Portanto, letras, números, conteúdo gráfico e instruções de programação são armazenadas em um computador em bytes.
A figura anterior que ilustra um componente de um computador construído com válvulas mostra uma unidade lógica que armazena um byte (8 bits).
Bem, voltando à pergunta inicial deste post, o que significa um HD ter 500 GB?

O sistema internacional de unidades adota os múltiplos:
k (quilo) = 1000
M (mega) = 1 000.000 (milhão)
G (giga) = 1.000.000.000 (bilhão)
T (tera) = 1.000.000.000.000 (trilhão)
Esses múltiplos são potências de 10, sendo adequados para o sistema decimal de numeração. No sistema binário, potências de 10 não têm qualquer significado especial. O que interessa são as potências de 2. No entanto, já que estamos acostumados a raciocinar com potências de 10, os engenheiros adotaram algumas potências de 2 que dão resultados muito próximos desses múltiplos, de forma que podemos avaliar quantidades como estamos acostumados.
Por exemplo:
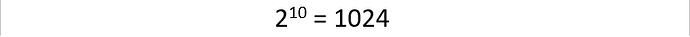
Essa é uma potência de 2 muito próxima de 1000. Essa quantidade de bytes foi batizada de 1 kilobyte. Para efeitos práticos, podemos pensar nela como sendo mil bytes sem muito erro de avaliação. Da mesma forma, há outras potências de 2 que são muito próximas de um milhão, um bilhão etc, que foram batizadas com os mesmos nomes dos múltiplos decimais do sistema internacional de unidades.
Sendo assim, vale a regra:
1 KB (kilobyte) é aproximadamente mil bytes;
1 MB (megabyte) é aproximadamente um milhão de bytes;
1 GB (gigabyte) é aproximadamente um bilhão de bytes;
1 TB (terabyte) é aproximadamente um trilhão de bytes.
Portanto, quando você compra um HD de 500 Gbytes, isso significa que ele consegue armazenar aproximadamente 500 bilhões de letras, números ou instruções de programação em linguagem de máquina.
Só para comparar, a circunferência do planeta Terra mede 49 mil km. Medida em milímetros, isso daria 49 bilhões de milímetros. Ou seja, um HD de 500 Gbytes armazena dados numa quantidade 10 vezes maior do que a medida da circunferência da Terra em milímetros.
Bastante, né?

I am an engineer, physics teacher, translator, and writer. I am also director of LatinLanguages, a translation agency that provides multilingual companies and final clients with translation into Portuguese and Spanish. If you work with these languages, we are your best option—delivering world-class service at Brazilian prices.
Marcos Chiquetto




